OSCILOSCOPIO

Un osciloscopio es un instrumento de medición electrónico para la representación gráfica de señales eléctricas que pueden variar en el tiempo. Es muy usado en electrónica de señal, frecuentemente junto a un analizador de espectro.
Presenta los valores de las señales eléctricas en forma de coordenadas en una pantalla, en la que normalmente el eje X (horizontal) representa tiempos y el eje Y (vertical) representa tensiones. La imagen así obtenida se denomina oscilograma. Suelen incluir otra entrada, llamada "eje Z" que controla la luminosidad del haz, permitiendo resaltar o apagar algunos segmentos de la traza.
Los osciloscopios, clasificados según su funcionamiento interno, pueden ser tanto analógicos como digitales, siendo el resultado mostrado idéntico en cualquiera de los dos casos, en teoría.
Contenido
· 1 Utilización · 2 Osciloscopio analógico... · 2.1 Limitaciones del osciloscopio analógico · 3 Osciloscopio digital · 4 Véase también · 5 Enlaces externos |
Utilización
En un osciloscopio existen, básicamente, dos tipos de controles que son utilizados como reguladores que ajustan la señal de entrada y permiten, consecuentemente, medir en la pantalla y de esta manera se pueden ver la forma de la señal medida por el osciloscopio, esto denominado en forma técnica se puede decir que el osciloscopio sirve para observar la señal que quiera medir.
El primer control regula el eje X (horizontal) y aprecia fracciones de tiempo (segundos, milisegundos, microsegundos, etc., según la resolución del aparato). El segundo regula el eje Y (vertical) controlando la tensión de entrada (en Voltios, milivoltios, microvoltios, etc., dependiendo de la resolución del aparato).
Estas regulaciones determinan el valor de la escala cuadricular que divide la pantalla, permitiendo saber cuánto representa cada cuadrado de esta para, en consecuencia, conocer el valor de la señal a medir, tanto en tensión como en frecuencia.
Osciloscopio analógico.
La tensión a medir se aplica a las placas de desviación vertical de un tubo de rayos catódicos (utilizando un amplificador con alta impedancia de entrada y ganancia ajustable) mientras que a las placas de desviación horizontal se aplica una tensión en diente de sierra (denominada así porque, de forma repetida, crece suavemente y luego cae de forma brusca). Esta tensión es producida mediante un circuito oscilador apropiado y su frecuencia puede ajustarse dentro de un amplio rango de valores, lo que permite adaptarse a la frecuencia de la señal a medir. Esto es lo que se denomina base de tiempos.
En la Figura 1 se puede ver una representación esquemática de un osciloscopio con indicación de las etapas mínimas fundamentales. El funcionamiento es el siguiente:
En el tubo de rayos catódicos el rayo de electrones generado por el cátodo y acelerado por el ánodo llega a la pantalla, recubierta interiormente de una capa fluorescente que se ilumina por el impacto de los electrones.
Si se aplica una diferencia de potencial a cualquiera de las dos parejas de placas de desviación, tiene lugar una desviación del haz de electrones debido al campo eléctrico creado por la tensión aplicada. De este modo, la tensión en diente de sierra, que se aplica a las placas de desviación horizontal, hace que el haz se mueva de izquierda a derecha y durante este tiempo, en ausencia de señal en las placas de desviación vertical, dibuje una línea recta horizontal en la pantalla y luego vuelva al punto de partida para iniciar un nuevo barrido. Este retorno no es percibido por el ojo humano debido a la velocidad a que se realiza y a que, de forma adicional, durante el mismo se produce un apagado (borrado) parcial o una desviación del rayo.
Si en estas condiciones se aplica a las placas de desviación vertical la señal a medir (a través del amplificador de ganancia ajustable) el haz, además de moverse de izquierda a derecha, se moverá hacia arriba o hacia abajo, dependiendo de la polaridad de la señal, y con mayor o menor amplitud dependiendo de la tensión aplicada.
Al estar los ejes de coordenadas divididos mediante marcas, es posible establecer una relación entre estas divisiones y el período del diente de sierra en lo que se refiere al eje X y al voltaje en lo referido al Y. Con ello a cada división horizontal corresponderá un tiempo concreto, del mismo modo que a cada división vertical corresponderá una tensión concreta. De esta forma en caso de señales periódicas se puede determinar tanto su período como su amplitud.
El margen de escalas típico, que varía de microvoltios a unos pocos voltios y de microsegundos a varios segundos, hace que este instrumento sea muy versátil para el estudio de una gran variedad de señales.
Limitaciones del osciloscopio analógico
El osciloscopio analógico tiene una serie de limitaciones propias de su funcionamiento:
· Las señales deben ser periódicas. Para ver una traza estable, la señal debe ser periódica ya que es la periodicidad de dicha señal la que refresca la traza en la pantalla.
· Las señales muy rápidas reducen el brillo. Cuando se observa parte del período de la señal, el brillo se reduce debido a que la tasa de refresco disminuye.
· Las señales lentas no forman una traza. Las señales de frecuencias bajas producen un barrido muy lento que no permite a la retina integrar la traza. Esto se solventa con tubos de alta persistencia. También existían cámaras Polaroid especialmente adaptadas para fotografiar las pantallas de osciloscopios. Manteniendo la exposición durante un periodo se obtiene una foto de la traza.
· Sólo se pueden ver transitorios si éstos son repetitivos.
Osciloscopio digital
En la actualidad los osciloscopios analógicos están siendo desplazados en gran medida por los osciloscopios digitales, entre otras razones por la facilidad de poder transferir las medidas a una computadora personal o pantalla LCD.
En el osciloscopio digital la señal es previamente digitalizada por un conversor analógico digital. Al depender la fiabilidad de la visualización de la calidad de este componente, esta debe ser cuidada al máximo.
Las características y procedimientos señalados para los osciloscopios analógicos son aplicables a los digitales. Sin embargo, en estos se tienen posibilidades adicionales, tales como el disparo anticipado (pre-triggering) para la visualización de eventos de corta duración, o la memorización del oscilograma transfiriendo los datos a un PC. Esto permite comparar medidas realizadas en el mismo punto de un circuito o elemento. Existen asimismo equipos que combinan etapas analógicas y digitales.
Estos osciloscopios añaden prestaciones y facilidades al usuario imposibles de obtener con circuitería analógica, como los siguientes:
· Medida automática de valores de pico, máximos y mínimos de señal. Verdadero valor eficaz.
· Medida de flancos de la señal y otros intervalos.
· Captura de transitorios.
· Cálculos avanzados, como la FFT para calcular el espectro de la señal.



 , se cumple que
, se cumple que 
 , se tiene que:
, se tiene que:




 .
.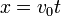


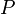 colocada a cierta distancia más allá de las placas.
colocada a cierta distancia más allá de las placas.



 Con ayuda de las densidades de carga se puede obtener la expresión del campo eléctrico creado por una distribución continua. Para ello consideramos un cuerpo con un determinado volumen V y una densidad volúmica de carga r . Si tomamos en cuenta un elemento diferencial de volumen, la carga almacenada valdrá dq = r·dv, y el campo creado por este elemento en un punto de observación, según la ley de Coulomb , valdrá
Con ayuda de las densidades de carga se puede obtener la expresión del campo eléctrico creado por una distribución continua. Para ello consideramos un cuerpo con un determinado volumen V y una densidad volúmica de carga r . Si tomamos en cuenta un elemento diferencial de volumen, la carga almacenada valdrá dq = r·dv, y el campo creado por este elemento en un punto de observación, según la ley de Coulomb , valdrá Para calcular el campo total debido a toda la distribución, y aprovechando el principio de superposición, hay que sumar todos las contribuciones de todos y cada uno de los elementos de volumen que forman el cuerpo cargado. Para ello habrá que hacer una suma integral:
Para calcular el campo total debido a toda la distribución, y aprovechando el principio de superposición, hay que sumar todos las contribuciones de todos y cada uno de los elementos de volumen que forman el cuerpo cargado. Para ello habrá que hacer una suma integral: Hay que tener en cuenta que tanto R como r dependen de la posición en el cuerpo y por lo tanto hay que párametrizar correctamente estas variables para poder efectuar la integración. Análogamente se pueden obtener las expresiones para distribuciones superficiales y lineales de carga:
Hay que tener en cuenta que tanto R como r dependen de la posición en el cuerpo y por lo tanto hay que párametrizar correctamente estas variables para poder efectuar la integración. Análogamente se pueden obtener las expresiones para distribuciones superficiales y lineales de carga:

 En este otro dibujo podemos ver como se forman las líneas de campo eléctrico en un dipolo. Como las dos cargas tienen el mismo valor el número de líneas de campo que salen de la carga positiva es igual al número de líneas que llegan a la carga negativa.
En este otro dibujo podemos ver como se forman las líneas de campo eléctrico en un dipolo. Como las dos cargas tienen el mismo valor el número de líneas de campo que salen de la carga positiva es igual al número de líneas que llegan a la carga negativa. En esencia, las líneas de campo señalan cómo se comportaría una carga eléctrica positiva cuyo valor es la unidad, cuando se introdujera en el dominio de acción del campo eléctrico representado.
En esencia, las líneas de campo señalan cómo se comportaría una carga eléctrica positiva cuyo valor es la unidad, cuando se introdujera en el dominio de acción del campo eléctrico representado. Observar como en esta última imagen el campo en la zona central, entre las cargas, es muy débil, las líneas están separadas, eso se debe a que en el centro el campo ejercido por una de las cargas se anula con el ejercido por la otra que es igual pero de sentido contrario.
Observar como en esta última imagen el campo en la zona central, entre las cargas, es muy débil, las líneas están separadas, eso se debe a que en el centro el campo ejercido por una de las cargas se anula con el ejercido por la otra que es igual pero de sentido contrario. 



 Asociando ambas relaciones:
Asociando ambas relaciones: Finalmente, se introduce una constante de proporcionalidad para transformar la relación anterior en una igualdad:
Finalmente, se introduce una constante de proporcionalidad para transformar la relación anterior en una igualdad:
 Dadas dos cargas puntuales y separadas una distancia en el vacio, se atraen o repelen entre sí con una fuerza cuya magnitud esta dada por:
Dadas dos cargas puntuales y separadas una distancia en el vacio, se atraen o repelen entre sí con una fuerza cuya magnitud esta dada por: La Ley de Coulomb se expresa mejor con magnitudes vectoriales:
La Ley de Coulomb se expresa mejor con magnitudes vectoriales: donde es un vector unitario que va en la dirección de la recta que une las cargas, siendo su sentido desde la carga que produce la fuerza hacia la carga que la experimenta.
donde es un vector unitario que va en la dirección de la recta que une las cargas, siendo su sentido desde la carga que produce la fuerza hacia la carga que la experimenta.




 Ejercicio 2
Ejercicio 2






