domingo, 21 de diciembre de 2008

Comportamiento de una carga punto en un campo eléctrico uniforme

Un campo eléctrico ejerce sobre una partícula cargada una fuerza \vec F= \vec E q

Esta fuerza produce una aceleración \vec a = \frac{\vec F}{m} siendo m la masa de la partícula.


Partícula moviéndose paralelamente al campo

Considérese una partícula de masa m y carga q que se suelta a partir del reposo en un campo entre dos placas paralelas cargadas tal como se muestra en la figura.

El movimiento es similar al de un cuerpo que cae en el campo gravitacional terrestre.

La aceleración está dada por a=\frac{F}{m}

Como \,\!F=qE, se cumple que a=\frac{qE}{m}

Aplicando las ecuaciones del movimiento uniformemente acelerado, como \,\!v_0=0, se tiene que:

v=at=\frac{qEt}{m}

Partícula moviéndose perpendicularmente al campo



y=\frac{1}{2}at^2=\frac{qEt^2}{2m}


v^2=2ay=\frac{2qEy}{m}

La energía cinética adquirida luego de recorrer una distancia y será;

K=\frac{1}{2}mv^2=\frac{1}{2}m\left ( \frac{2qEy}{m} \right )=qEy




La figura muestra un electrón de masa m y carga e que es disparado con una velocidad v0 perpendicularmente a un campo uniforme \vec E.

El movimiento es similar al de un proyectil disparado horizontalmente en el campo gravitacional terrestre. En consecuencia el movimiento horizontal x y el vertical y están dados por las expresiones:

\,\!x=v_0t


y=\frac{1}{2}at^2=\frac{eE}{2m}t^2

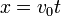
Sustituyendo a t se obtiene:

y=\frac{eE}{2m{v_0}^2}x^2

que es la ecuación de la trayectoria.

Cuando el electrón sale de entre las placas, lo hace en una trayectoria recta tangente a la parábola en el punto de salida y puede hacerse llegar a una pantalla fluorescente 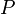\,\!P colocada a cierta distancia más allá de las placas.


Publicado por en

1 comentario:

Suscribirse a: Enviar comentarios (Atom)